MATEMATICA
Le funzioni a due variabili e le equazioni differenziali

Le funzioni a due variabili
Le equazioni differenziali
- Definizione di equazione differenziale
- Equazioni differenziali del primo ordine: immediate, a variabili separabili e lineari
- Equazioni differenziali del secondo ordine: lineari a coefficienti costanti omogeneo
- Equazioni differenziali del secondo ordine: linea a coefficienti costanti completo
Una “funzione reale di due variabili reali” è una corrispondenza che associa ad ogni coppia di numeri reali (x ; y), una ed una sola variabile z. Per indicare quindi che una data funzione f associa alla coppia (x ; y) il valore z, si potrà scrivere come
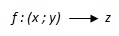 |
o anche come
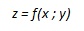 |
Da questa formula si possono ricavare sia la forma “esplicita” che quella “implicita” della funzione, che sono rispettivamente
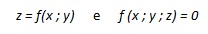 |
Il numero reale z si dice “immagine” della coppia (x ; y), mentre la coppia formata dalle sue coordinate cartesiane si dice “controimmagine” del valore z.
Il dominio di una funzione di due variabili è quindi rappresentato graficamente da un sottoinsieme del piano cartesiano.
Il “codominio” della funzione f, invece, è l’insieme dei valori che assume la variabile z cha hanno almeno una controimmagine (x ; y) ∈ D.
La ricerca del dominio di una funzione di due variabili si riconduce spesso alla risoluzione di equazioni, disequazioni o sistemi in due variabili; è opportuno perciò rappresentare tale dominio come sottoinsieme del piano cartesiano. Come per le funzioni di una variabile, la determinazione del codominio di una funzione di due variabili è spesso problematica. Pertanto, salvi casi particolari, non è richiesta la ricerca ed il calcolo del codominio.
Per determinare il dominio di una funzione a due variabili, bisogna per prima cosa porre le condizioni di esistenza della funzione considerata; dopodiché, rendere la disequazione una “equazione associata”, sostituendo al segno di maggioranza o minoranza il segno di uguaglianza. Così facendo, si ottiene la “frontiera” della funzione. Disegnata ora sul grafico cartesiano la frontiera, verificare per quali punti (x ; y) si verifica la disequazione, sostituendo appunto nella disequazione un punto (x ; y) a scelta, e se questo punto verifica la disequazione, tutti i punti di quella parte di piano verificano la disequazione e quindi appartengono al dominio. Se invece il punto (x ; y) scelto non verifica la disequazione, tutti i punti appartenenti a quella parte di piano non verificano la disequazione e di conseguenza non appartengono al dominio.
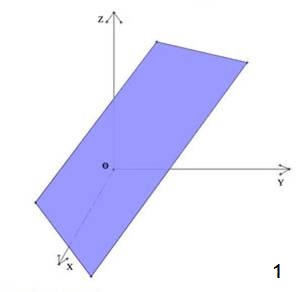
Non è difficile definire ora in modo analogo il grafico di una funzione di due variabili: definita f(x ; y) una funzione di due variabili, il grafico di questa funzione è una superficie nello spazio costituita dai punti P(xo ; yo ; zo), e zo = f(xo ; yo), che è l’immagine.
Si passa quindi da una figura bidimensionale di una funzione di una variabile ad una figura tridimensionale, con l’aggiunta di una nuova variabile z.
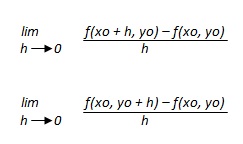 |
aventi rispettivamente risultati uguali a f'x (xo, yo) ed f'y (xo, yo).
Le regole di derivazione usate per risolvere le funzioni ad una variabile, valgono anche per le funzioni a due variabili perché, quando si calcola la derivata parziale, una variabile rimane costante ed una si comporta appunto da variabile.
Si passa ora al calcolo della “matrice hessiana” della funzione, ovvero la matrice quadrata n × n delle derivate parziali seconde della funzione; si calcolano quindi le derivate parziali seconde, ovvero le derivate parziali delle derivate parziali, e si mettono in ordine nella matrice hessiana, nel seguente modo:
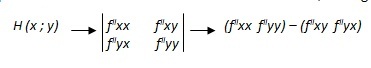 |
Il risultato ora dell’hessiano (f''xx f''yy) – (f''xy f''yx) avrà come totale una funzione, alla quale si andranno a sostituire i punti stazionari calcolati prima, e si otterrà così come risultato un numero che potrà essere maggiore, uguale o minore di zero:
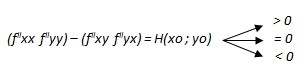 |
Se questo numero H(xo ; yo) è:
> 0 ed f''xx(x ; y) < 0, il punto P(xo, yo, xo) sarà un “punto di massimo” MAX, ovvero un punto in cui la funzione si trova sempre al di sotto;
> 0 ed fIIxx(x ; y) > 0, il punto P(xo, yo, xo) sarà un “punto di minimo” MIN, ovvero un punto in cui la funzione si trova sempre al di sopra;
< 0, il punto P(xo, yo, xo) sarà un “punto di sella”, ovvero un punto intorno al quale la funzione può stare sia al di sopra che al di sotto;
= 0, infine, il punto P(xo, yo, xo) risulta un punto indeterminato.
Com’è noto, un piano parallelo al piano coordinato xz avrà equazione y = k, essendo k una costante; allo stesso modo l’equazione x = k definisce un piano parallelo al piano coordinato yz.
Si può allora dire che il “grafico sezione” è una linea ottenuta dall’intersezione del grafico di una funzione con un piano parallelo ai piani di coordinate xz ed yz.
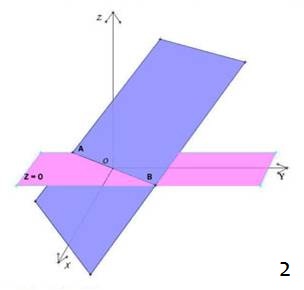
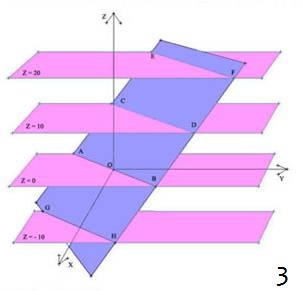
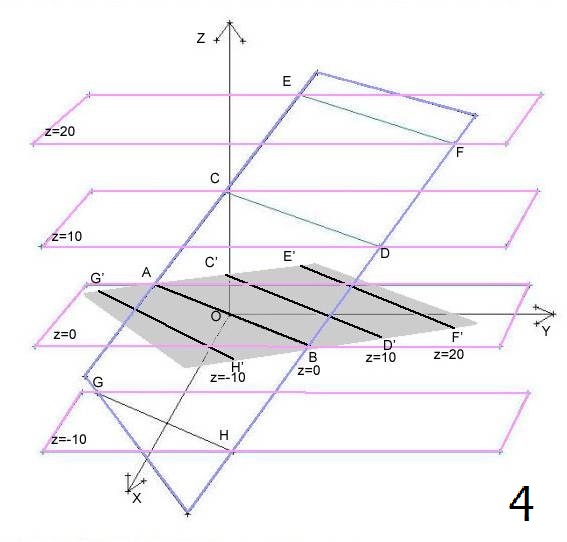
Le “linee di livello” o “curve di livello” di una funzione a due variabili si ottengono sezionandone il grafico con i piani paralleli al piano xy;
ciascuno di tali piani è il luogo geometrico dei punto dello spazio aventi quota uguale ad una costante k, e può perciò essere scritta sottoforma di equazione come z = k. Una curva di livello è perciò costituita dall’insieme dei punti del grafico della funzione aventi tutti la stessa quota, uguale ad una prefissata costante k. Se l’equazione della funzione è
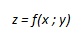 |
le coordinate dei punti della curva di livello k sono caratterizzate dalle relazioni
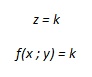 |
Concludendo, si può quindi dire che la linea di livello è quella linea ottenuta dall’intersezione del grafico della funzione con un piano parallelo al piano xy.
 |  |
 |  |
L’equazione del tipo
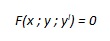 |
si dice “equazione differenziale del primo ordine”, mentre l’equazione del tipo
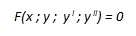 |
Si dice “equazione differenziale del secondo ordine”.
In generale si può dire che una relazione tra la variabile indipendente x, una funzione incognita y e le sue derivate successive fino a quella di ordine n, del tipo
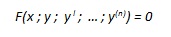 |
viene detta “equazione differenziale dell’n-esimo ordine”, o di ordine n.
La soluzione si chiama “integrale generale” o “soluzione generale” quando vi è la costante k; se alla costante k viene assegnato un particolare valore, la soluzione si chiama “integrale particolare”.
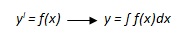 |
dove per trovare la soluzione y bisogna calcolare l’integrale della funzione f(x).
Le equazioni, poi, dette “a variabili separabili”, sono quelle in cui per calcolare la soluzione si può porre
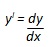 |
Per trovare la soluzione, si sostituisce quindi ad y' il rapporto fra dy e dx; dopodiché, si prosegue portando da un lato del segno “=” tutti i termini con la x ed all’altro lato tutti i termini con la y; una volta ordinata l’equazione, si fanno i due integrali, ovvero quello a destra dell’uguale e quello a sinistra dell’uguale, e quindi l’integrale rispetto ad x e l’integrale rispetto ad y. Una volta calcolati i due integrali si può risalire al risultato, ovvero alla funzione y = f(x).
Vi sono poi le “equazioni lineari” del primo ordine, che sono quelle del tipo
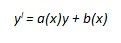 |
dove a(x) e b(x) sono funzioni continue in un opportuno intervallo. Ponendo b(x)= 0, risulterebbe un’equazione a variabile separabili, che si può facilmente risolvere ponendo y' come il rapporto fra dy e dx. Diventa così
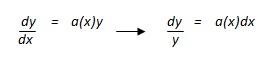 |
Detta A(x) una primitiva qualsiasi della funzione a(x) e c una costante arbitraria, si ottiene, dopo il calcolo degli integrali
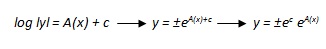 |
Dato che c è una costante arbitraria, ±ec risulta un numero reale diverso da zero e quindi l’ultima equazione scritta diventa y = ± keA(x) con k ? 0.
Applicando ora il metodo di Lagrange, o metodo della variazione della costante arbitraria, che consiste nel rendere la costante k una funzione, si ottiene y = k(x)eA(x) e ricordando che A(x) è primitiva di a(x), ovvero A'(x) = a(x), si ricava
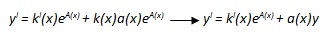 |
Sostituendo poi nella prima espressione, ovvero y' = a(x)y + b(x), le espressioni di y ed y', che sono rispettivamente k(x)eA(x) e k'(x)eA(x) + a(x)y, si ottiene
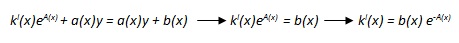 |
Quindi per calcolare k(x) bisogna fare l’integrale di b(x)e-A(x), dato che k'(x) è una primitiva di b(x)e-A(x), e allora si avrà
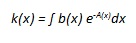 |
e siccome y = k(x)eA(x) e k(x) = yeA(x), la formula k(x) = ∫ b(x) e-A(x)dx diventa
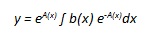 |
Riassumendo:
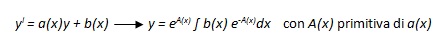 |
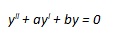 |
Per determinare l’integrale generale di tale equazione si deve innanzitutto risolvere, rispetto all’incognita ausiliaria k, l’equazione “caratteristica”, ossia
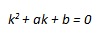 |
Questa è un’equazione algebrica di secondo grado, il cui discriminante è Δ = a2 – 4b; tale equazione si ottiene dalla prima sostituendo alla funzione y un’incognita k con esponente uguale all’ordine di derivazione. Si distinguono tre casi, che andremo a descrivere dopo aver indicato con c1 e c2 le due costanti arbitrarie.
1° caso :Δ > 0
L’equazione ha come soluzione due radici reali e distinte; siano k1 e k2 tali radici, il risultato dell’integrale generale sarà
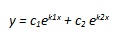 |
2° caso : Δ = 0
In questo caso le radici sono coincidenti: k1 = k2 = -a/2. Posto -a/2 = k, l’integrale generale dell’equazione sarà
 |
3° caso : Δ < 0
In questo caso l’integrale ha come soluzioni due radici complesse coniugate α ± jβ, con α = -a/2, e β = √Δ / 2. L’integrale generale dell’equazione sarà quindi
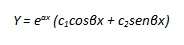 |
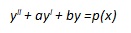 |
dove p(x) è una funzione continua, non nulla, in un opportuno intervallo. Chiameremo equazione “associata” alla prima l’equazione
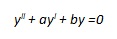 |
ottenuta dalla prima ponendo uguale a zero il secondo membro; l’equazione passa così da completa ad omogenea. Calcolata poi la soluzione dell’equazione omogenea, si ottiene che y = SOLUZIONE OMOGENEA + q(x), dove q(x) rappresenta un polinomio che verrà poi calcolato. Il grado di q(x), indicato con la lettera m, dipende dal grado di p(x), indicato con la lettera n e dai coefficienti a e b dell’equazione; infatti
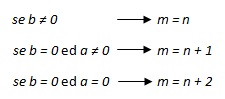 |
Trovato il grado m di g(x), bisognerà trovare le funzioni q(x), q'(x) e q''(x); ad esempio, sia il grado della funzione q(x) uguale a 2, e quindi m = 2, la funzione sarà
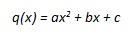 |
e le sue derivate, prima e seconda, saranno rispettivamente
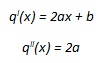 |
Infine, bisogna sostituire ad y'' e ad y' della funzione iniziale, le due derivate appena calcolate, ovvero q''x ed qìx; si otterrà così l’equazione finale, che nel caso analizzato, ovvero nel caso di m = 2, sarà
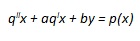 |
Trovata l’equazione, bisogna calcolare ora i coefficienti a e b mediante un sistema, che verranno poi sostituiti nella funzione q(x) della “soluzione omogenea”; sostituendo poi la funzione q(x) con i risultati dei coefficienti, si ottiene la soluzione finale, detta “soluzione completa”.